Exploring Binary Search
Understanding binary search in Python
Introduction
Binary search, a searching algorithm, stands out for its efficiency in locating an item within a sorted list. In contrast to Linear Search, which progresses sequentially through each item, binary search strategically narrows down the search space by repeatedly halving it until the target item is found. To illustrate, consider the classic guessing game where a friend attempts to guess a number you've secretly chosen within a given range. Binary search mimics this process by intelligently eliminating half of the possible numbers with each guess.
Time and Space Complexity
Binary search's efficiency is not only evident in its intuitive approach but also in its time complexity. The time complexity of binary search is O(log n), where n is the number of elements in the sorted list. This logarithmic time complexity makes binary search significantly faster than linear search, especially as the size of the dataset increases.
In terms of space complexity, binary search is minimal. It operates with constant space requirements, denoted as O(1), as it doesn't require additional storage proportional to the input size. This makes binary search not only time-efficient but also memory-efficient, particularly in scenarios where resources are a crucial consideration.
Dive into the Code
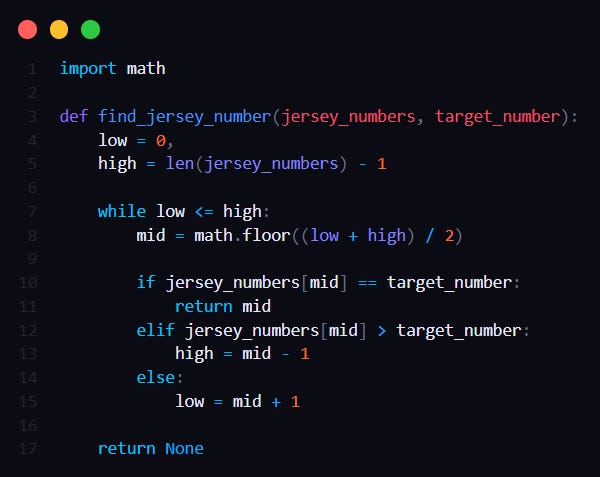
Let's explore a practical example in Python inspired by my passion for basketball. Imagine you have a sorted list of basketball players' jersey numbers: [8, 13, 23, 34, 44, 55, 77]. Your goal is to find the jersey number 23 (for obvious reason's 🐐) using binary search.
**Note:** Binary search requires a pre-sorted dataset to function optimally. Now, let's embark on the search.
Initialization
- Begin with two pointers, low and high, representing the start and end of the list, respectively.
- The target number to be found is provided.
Binary Search
As long as low is less than or equal to high, indicating the pointers:
- Calculate the middle index, `mid`, using floor division of the sum of low and high by 2.
- Compare the number at the middle index (jersey_numbers[mid]) with the target.
- If they match, return mid as the target is found.
- If jersey_numbers[mid] is bigger than the target number, we know the target must be in the left half. So, we shift our focus to the left side by updating high to be one less than the middle (mid - 1).
- If smaller, we understand the target is in the right half. To narrow our search to the right side, we update low to be one more than the middle (mid + 1).
Completion
If the loop concludes without finding the target, we can return `None` to indicate its absence in the list.
Python Code
Here's a brief visualization of how this works:
If you're interested in playing with this interactive visualizer to further understand the dynamics of binary search, check out the
Conclusion
In essence, binary search proves to be a powerful and efficient method for locating items in a sorted dataset. Its ability to systematically narrow down the search space sets it apart from linear search, showcasing superior performance, especially with large datasets.
The example using basketball jersey numbers illustrated the algorithm's key phases, providing a clear understanding of its implementation.
Mastering binary search goes beyond finding numbers in a list; it's about adopting a versatile approach to problem-solving applicable across various scenarios. As you navigate the realms of algorithms and software development, remember the efficiency and adaptability that binary search brings to the table.
Thanks for reading. Please share and subscribe 😁 Until next time